Chapitre 1 : L'ensemble des réels

Icône de l'outil pédagogique Question Choix Multiple
Les propositions suivantes définissent une relation d'ordre  R1 :
  
(x,y) ² xR1y x y
(x,y) ² xR1y x y
(x,y) ² xR1y x > y
(x,y) ² xR1y x > y

Sélection multiple
La valeur absolue est définie comme :

x |x|=

x |x|=()²
x |x|=
x |-x|=max(-x,x)
x |-x|=min(-x,x)



Icône de l'outil pédagogique Question Choix Multiple
Le produit de deux valeurs absolues |x| et |y| est…
  
Supérieur à la valeur absolue du produit xy
Egal à la valeur absolue du produit xy
Inferieur à la valeur absolue du produit xy

Sélection multiple
Les ensembles suivants sont des intervalles :
*
[0 ; 1[
{0 , 1}
[0 ; 6[ [5,7]



Icône de l'outil pédagogique Question Choix Multiple
Une union d’intervalle…
  
Est forcément un intervalle
Peut être un intervalle
N’est jamais un intervalle

Icône de l'outil pédagogique Question Choix Multiple
La partie entière de tout réel x…
  
est le plus petit entier majorant de x
est le plus grand entier majorant x
est le plus petit entier minorant x
est le plus grand entier minorant x

Sélection multiple
La partie entière a comme propriétés :
E(x) x <E(x)+1
E(x)-1 < x E(x)
x-1 < E(x) x
x E(x) < x+1



Sélection multiple
Les sous-ensembles suivants sont-ils denses dans ?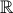
L’ensemble des nombres rationnels
L’ensemble des entiers naturels
L’ensemble des entiers relatifs
L’ensemble des nombres irrationnels c



Icône de l'outil pédagogique Question Choix Multiple
Pour tout X partie non vide de 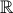, on dit que X est borné si :
  
(m, M)² xX
(m, M)² xX
(m, M)²    xX 

Sélection multiple
Pour tout WP( ), on dit que W est :
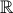
un voisinage d'un réel x0 si, et seulement si, il existe un réel a strictement positif tel que l’intervalle ouvert ]x0-a, x0+a[ est inclus dans W
un voisinage d'un réel x0 si, et seulement si, il existe un réel a positif tel que l’intervalle fermé [x0-a, x0+a] est inclus dans W